标签:神经科学启发工业故障诊断
前言
《Brain-Inspired Meta-Learning for Few-Shot Bearing Fault Diagnosis》
期刊:IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS
年份:2025
分区:Q1,一区Top;IF:8.9
- 把“突触可塑性规则”本身纳入元学习框架,从而让模型在少样本任务中既学得快,又学得稳。
- 在真实工业 / 神经工程场景中(轴承、EEG 都一样):新工况 / 新被试下,故障 / 意图样本 极少,深度模型 → 严重过拟合 ➡️ 这是一个标准 few-shot + domain shift 问题。
- 明确指出:不是模型不够深,而是学习机制不对。
一、研究背景与问题定位
1. 工业实际痛点
- 数据稀缺性: 真实工业场景中,复杂机械结构和恶劣工作环境导致故障数据采集困难、故障难以复现。
- 传统深度学习的局限: 需要大量标注数据,在小样本场景下易过拟合,无法提取有效特征。
2. 现有解决方案的缺陷
作者系统梳理了四类小样本故障诊断方法:
- 迁移学习Transfer Learning:依赖任务分布相似性,距离函数设计困难,工况一变就失效
- 数据增强Data Augmentation(GAN):模型训练不稳定,生成样本质量难保证
- 度量学习Metric Learning:过度依赖相似性函数设计
- 元学习Meta-Learning:仍是BP,本质“学的快但不稳”,MAML等方法对复杂任务学习能力不足、训练困难
3. 神经科学启示
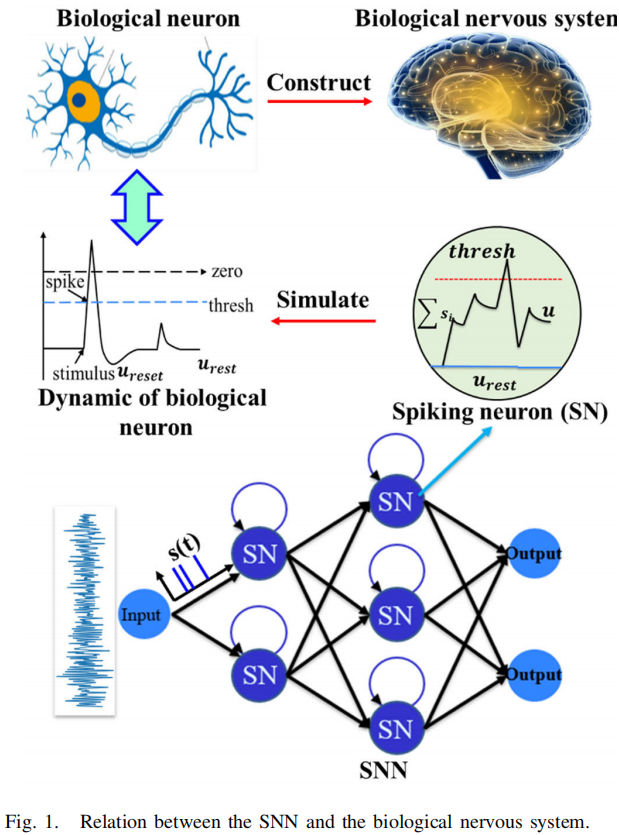
- 生物大脑的小样本优势: 海马体的全局-局部并行学习机制具有强大的小样本学习能力
- 脉冲神经网络: 模拟生物神经系统,用脉冲序列传递信息,但脉冲的非连续性使其难以直接应用反向传播
- 核心思想: 少样本学习不是“少数据问题”,而是“学习机制问题”,这就是转向 生物神经系统(SNN + STDP) 的根本原因
二、方法主线(三层递进结构)
层 1:为什么用 SNN(不是为了新潮)
作者强调的是:
- SNN ≠ ANN
- *NN 是 动态系统
- spike timing 本身就适合 少样本、时序结构学习
但作者并不满意现有 SNN 的训练方式。
层 2:为什么现有 SNN 学得“不像大脑”
虽然是 SNN,但大多数方法:
- 用 surrogate gradient
- 本质还是 BP 的近似
👉 生物结构对了,学习机制错了
这是作者提出 brain-inspired weight-updating approach 的直接动机。
层 3:为什么还要 Meta-learning
即便你有 STDP:
- STDP 是 局部
- 无法保证 新任务快速收敛
而生物大脑能做到:
在“相似经验”基础上,几次刺激就学会新任务
➡️ 这正是 Meta-learning 的生物动机
三、核心方法
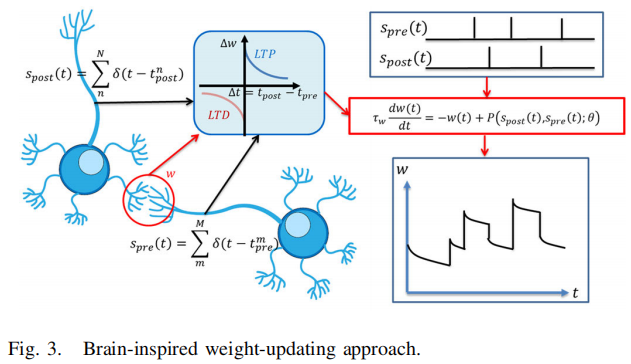
1.Brain-Inspired Weight-Updating(真正的技术点)
1️⃣ 权重不是一个东西,而是两个通道
作者明确写出(非常重要):$w = w_u + w_s$
$w_u$:无监督 STDP(结构、自组织)
$w_s$:有监督 STBP(判别、目标)
👉 这是整篇文章的“力学结构”
2️⃣ STDP 的建模方式很聪明
作者没有用复杂生物模型,而是:
把连续 STDP 微分方程改写为 时间迭代形式(适合 SNN 仿真)
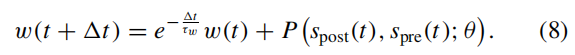
并设计了一个 兼顾 spike + membrane potential 的 STDP 函数。
这是一个非常“工程友好”的生物建模。
3️⃣ θ 的引入是隐藏亮点
- θ 是 STDP 的超参数
- 作者将其解释为 top-down neuromodulatory signals
这一步让: - STDP 不再是“固定规则”
- 而是 可学习、可调制的
➡️ 为后面的 meta-learning 铺路
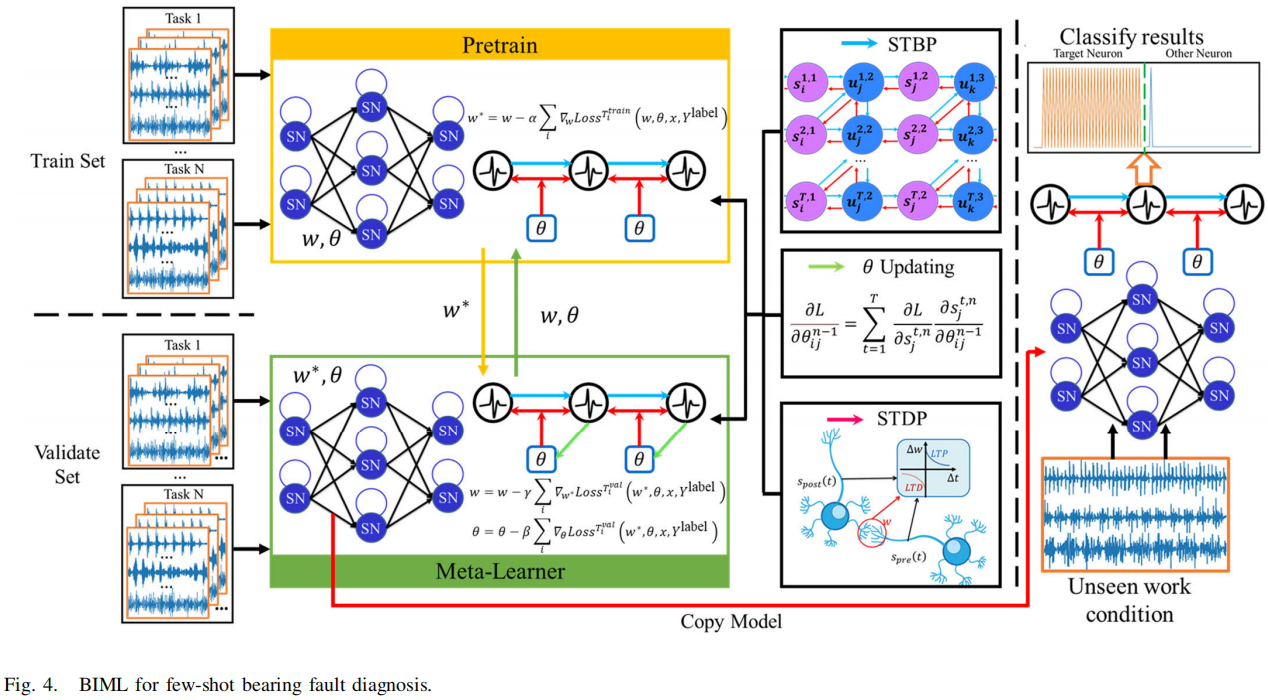
2.Meta-Learning Strategy(BIML 的本体)
1️⃣ BIML 不是“在 SNN 上套 MAML”
这是最容易被误解的地方。
MAML 学什么?
- 学初始化权重
BIML 学什么? - 学初始化权重 +
- 学 突触可塑性规则的调制参数 θ
- 👉 学习对象升维了
2️⃣ BIML 的三阶段结构非常清晰
作者把流程拆成:
- Pretraining(任务内适应)
- Meta-learning(跨任务更新初始化)
- Fine-tuning(目标任务 few-shot)
而且每一阶段都 显式用 STDP + STBP
这点在 TNNLS 审稿里是非常加分的(机制一致性)。

3️⃣ 数学上,BIML 在“偷偷干一件很重要的事”
在讨论部分,作者给出一个非常关键的解释:
- STDP 在 meta-learning 中等价于引入“隐式损失项”
这个隐式损失会: - 增大类间距离
- 减小类内距离
➡️ 这解释了为什么 BIML 比 SML / GMAML 稳
这不是拍脑袋,而是有推导 + 可视化验证。
四、实验设计与验证
1.数据集构建
- 双转子试验台:模拟航空发动机复杂工况
- 轴间轴承(内/外圈同向旋转)
- 4种工况(转速组合)
- 9种健康状态(正常+3种故障×不同程度)
- 传统轴承试验台:基础验证
- 4种转速工况
- 9种健康状态
数据处理:
- 滑动窗口(1024点,无重叠)
- 每工况每状态100个样本
- 9-way K-shot划分(K=1或5)
数据设计是“反深度学习直觉的”
Meta-train:低速工况
Meta-test:高速工况(更难)
👉 这是对模型泛化能力的“反向测试”
2. 对比方法选择
全面覆盖四类小样本方法:
- 数据增强:WGAN, MCGM
- 迁移学习:DAL, MSDA
- 元学习:SML, GMAML
- SNN基线:ISNN, MLSNN
3. 核心实验结果
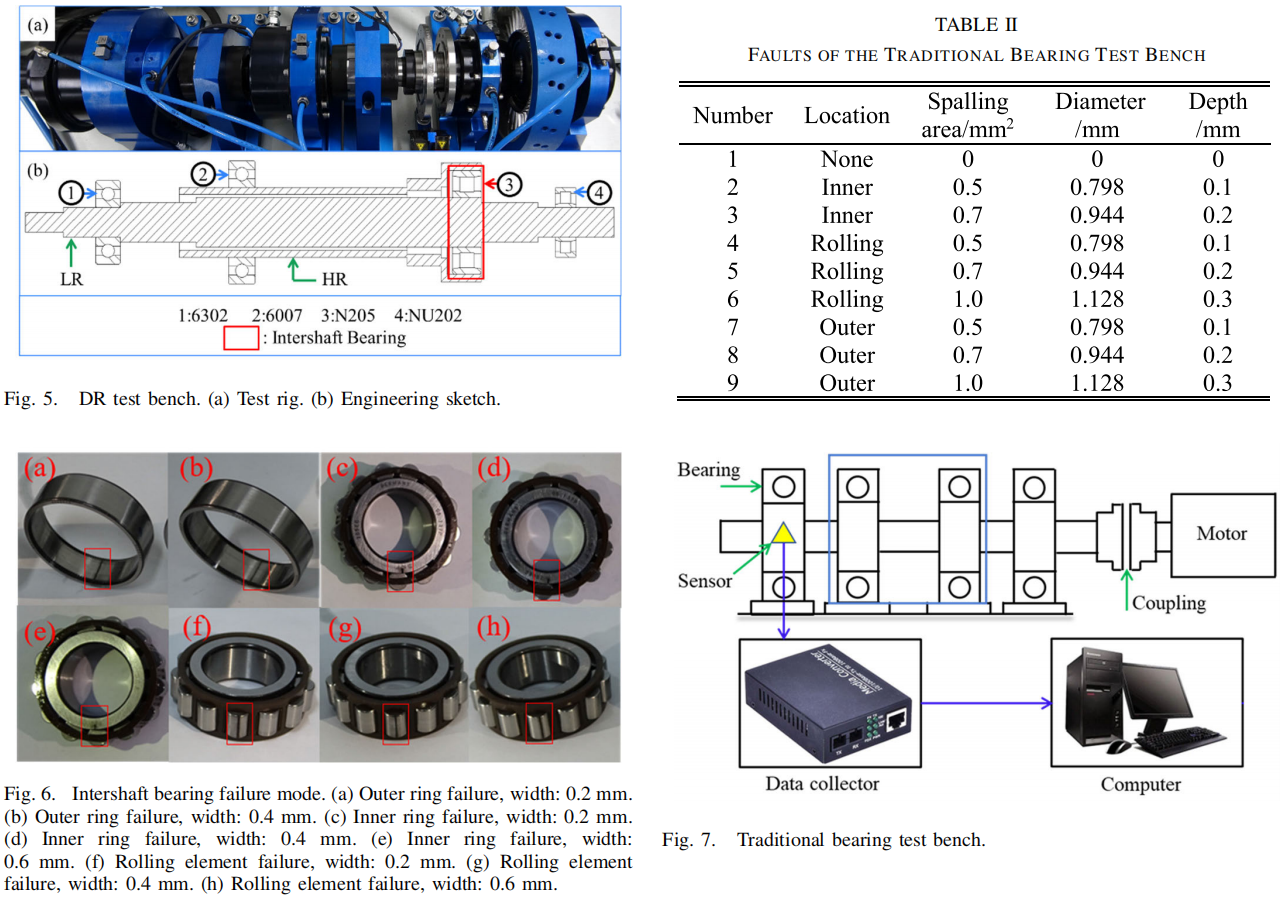
表V-VI 结果分析:
- BIML在所有任务上全面领先
- 9-way 5-shot任务优势更明显(DR台:99.60% vs SML 95.78%)
- 验证了脑启发机制与元学习结合的协同效应
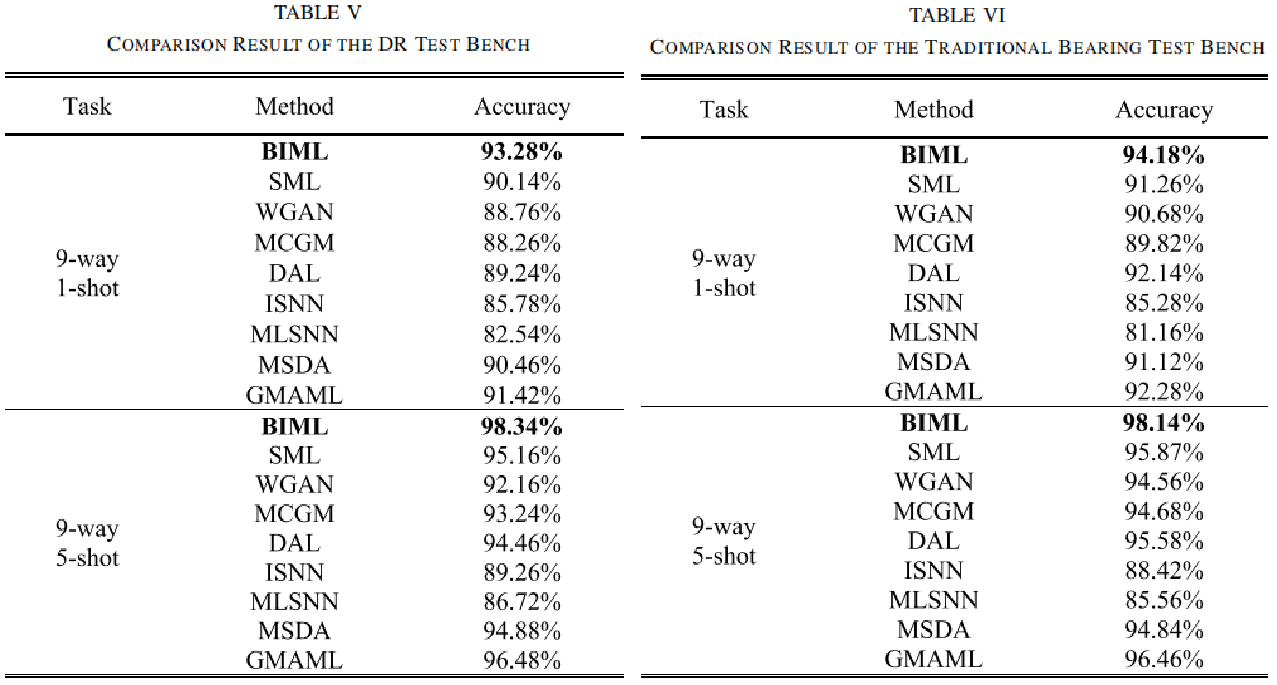
图8 适应步数分析:
- BIML达到最优性能所需步数更少(1-shot:20步 vs SML 25+步)
- 收敛速度更快,计算成本更低
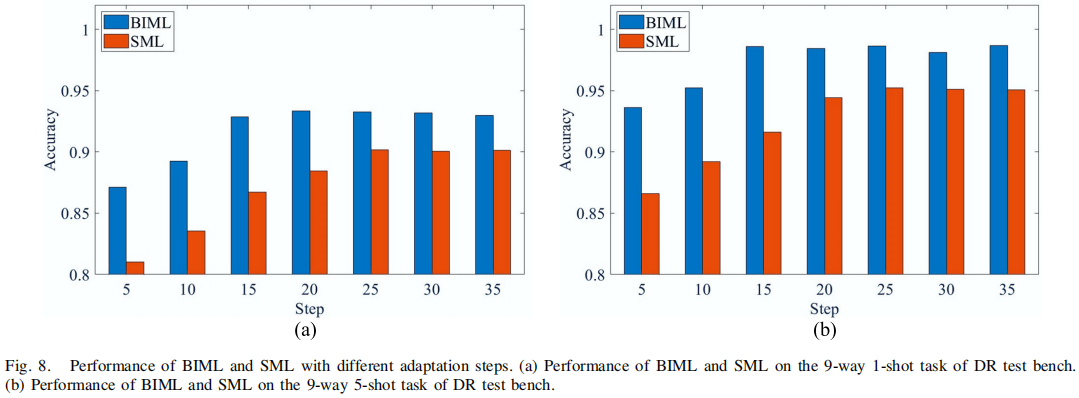
图9 脉冲输出可视化:
- BIML目标神经元响应率上升更快、更稳定
- 非目标神经元抑制更彻底
- 体现了更好的类间分离能力
五. 深入分析与讨论
1. 理论有效性分析
作者尝试从理论上解释BIML优势:
- 将无监督STDP重写为隐式损失函数
- 推导显示STDP引入的惩罚项有助于:
- 增大类间间距:$(\mathbf{c}_q^T \tilde{\mathbf{x}})^2$
- 减小类内间距:$(1 - \mathbf{c}_i^T \tilde{\mathbf{x}})^2$
2. 实验验证理论
- 图10特征可视化:BIML特征聚类更紧密、类间分离更明显
- 图11混淆矩阵:BIML错误主要是同类故障的程度误判,而非不同位置故障的混淆
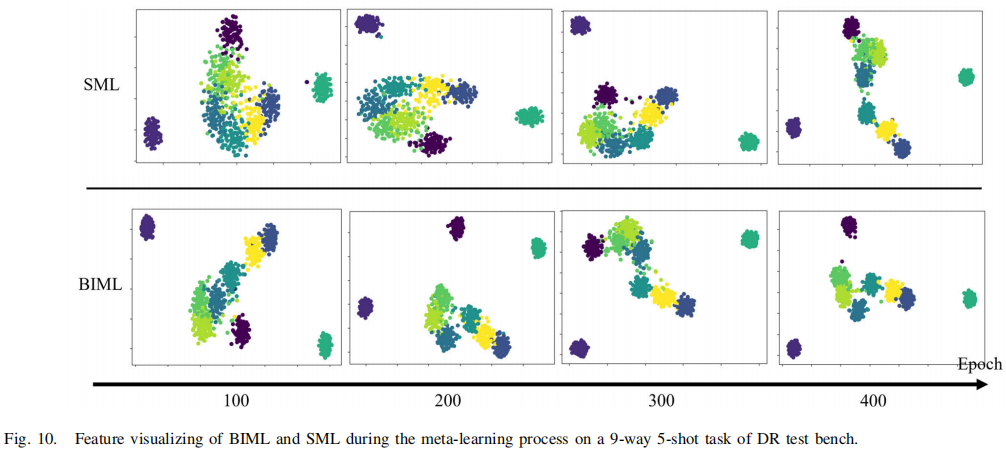
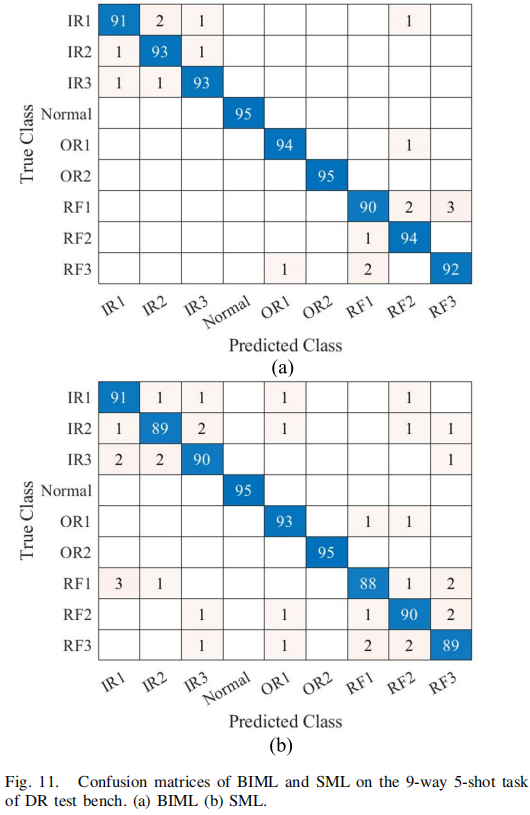
3. 消融实验
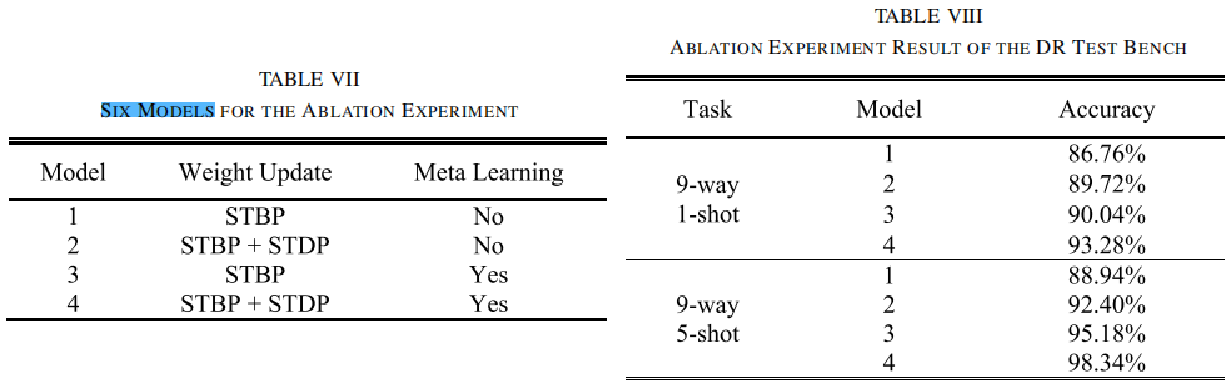
表VII-VIII结果:
- STDP单独贡献:模型2 vs 1(+3-4%)
- 元学习单独贡献:模型3 vs 1(+5-6%)
- 两者结合:模型4(BIML)效果最佳
- 元学习的贡献略大于STDP,但两者协同效果远超单一模块
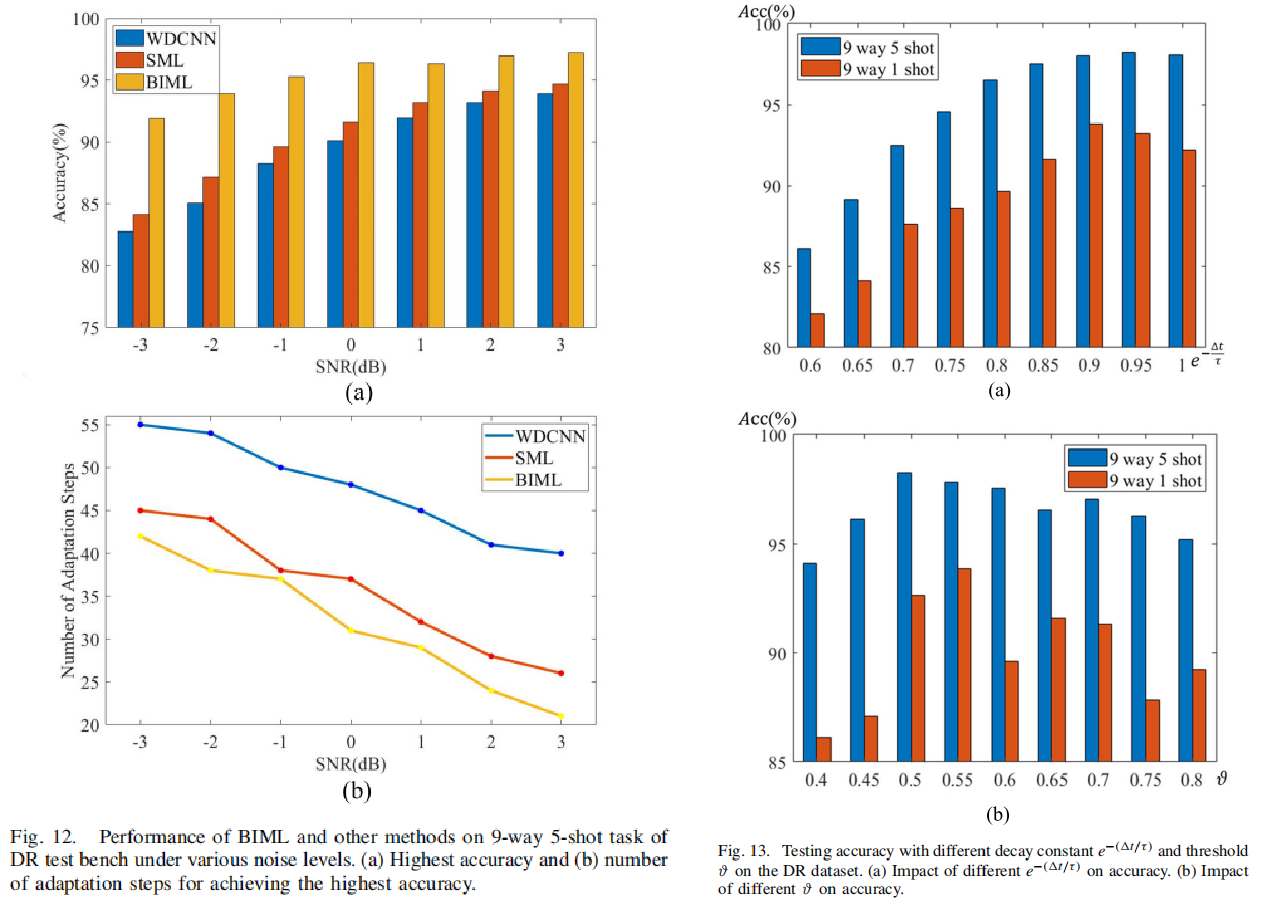
5. 超参数敏感性
- 最优参数在不同任务间相近但不同
- 采用折中值$(e^{-\Delta t / \tau} = 0.95, \quad \vartheta = 0.5
)$仍取得优异性能 - 说明方法对超参数不敏感,易于应用
六. 文章亮点
1️⃣ 少样本的关键不是模型复杂度,而是“可塑性结构”
BIML 强不是因为 SNN,而是因为:
把“怎么学”本身当成学习对象
2️⃣ STDP = 结构正则,而不是噪声
很多人误解 STDP 是“弱规则”,
但在这篇文章里,它是:
一个隐式的、与任务无关的结构约束
3️⃣ Meta-learning 的层级可以比“权重”更高
BIML 给了你一个非常重要的启示:
Meta-learning 不一定学模型参数,也可以学“学习规则”
七、评价与学术贡献
技术贡献
- 首个脑启发的少样本轴承诊断框架:将神经科学原理系统化引入工业故障诊断
- 新型SNN训练范式:绕过脉冲非连续性问题,通过STDP与梯度下降耦合实现高效学习
- 双层优化元学习:创新的参数更新策略,真正实现了“学会如何学习”
理论意义
- 连接神经科学与AI:为类脑计算在工业应用提供了可行路径
- 小样本学习新思路:证明生物学习机制在数据稀缺问题上的优越性
- 可解释性增强:相比黑盒深度网络,BIML具有更强的生物可解释性
实用价值
- 工业友好性:对噪声鲁棒、适应步数少、计算成本低
- 泛化能力强:在双转子和传统轴承台均表现优异
- 解决真实痛点:直接针对工业数据稀缺的核心挑战
八、局限性与未来方向
局限性
- 任务分布假设:依赖元训练任务与目标任务的相似性
1. STDP 形式仍是手工设计的
*** θ 只调参数,不调函数形式**- 任务相似性默认存在
- 没有讨论 task mismatch 的极端情况
- 任务相似性默认存在
- 计算复杂度:元学习阶段需要大量任务采样
- SNN 计算成本仍偏高
- 理论推导近似:有效性分析包含较多近似假设
未来方向
- 在线元学习:适应动态变化的工业环境
- 跨模态融合:结合振动、声学、温度等多源信号
- 硬件实现:利用神经形态芯片实现低功耗部署
- 理论深化:建立更严谨的数学框架
总结
这篇论文代表了故障诊断领域的前沿研究方向,成功地将:神经科学原理(海马体学习机制),新型神经网络(脉冲神经网络),先进学习范式(元学习)三者有机融合,创造性地解决了工业小样本故障诊断这一关键难题。其方法论的系统性、实验的严谨性、以及理论与实践的紧密结合,使其成为该领域的标杆性工作,为后续研究提供了重要参考范式。
论文不仅提出了一个高性能算法,更重要的是开辟了一条神经科学启发的人工智能在工业应用的新路径,具有深远的学术和工程价值。
补充知识
1. 元学习(Meta-Learning)
元学习(Meta-Learning)被称为“学会学习的学习”,是一种让模型能够快速适应新任务的学习范式。与传统深度学习需要大量数据从头训练不同,元学习的目标是训练模型在少量样本下快速学习新任务。
- 核心思想
元学习通过在多个相关任务上进行训练,让模型掌握如何快速学习的能力,当遇到新任务时,只需要少量数据和几步调整就能获得良好性能。 - 主要策略类型
- 基于优化的元学习(Optimization-based)
核心思想:学习一个良好的初始化参数,使模型只需少量梯度步就能适应新任务
代表算法:MAML(Model-Agnostic Meta-Learning):学习一组初始参数,使从该点出发,对新任务进行少量梯度更新就能达到好效果 - 基于度量的元学习(Metric-based)
核心思想:学习一个度量空间,通过相似度比较进行预测
代表算法:
Siamese Networks:学习输入之间的相似度函数
Matching Networks:使用注意力机制将支持集和查询集关联
Prototypical Networks:为每个类别计算原型表示,通过距离分类 - 基于模型的元学习(Model-based)
核心思想:设计能够快速适应的模型架构,通常使用内部记忆机制
代表算法:
Memory-Augmented Neural Networks:添加外部记忆模块
Meta Networks:结合慢权重(长期知识)和快权重(快速适应)
LSTM Meta-Learner:用LSTM学习优化算法
- 基于优化的元学习(Optimization-based)
- 典型应用场景
- 小样本学习(Few-shot Learning)
N-way K-shot问题:从每个类别K个样本中学习N类分类 - 快速适应
机器人控制策略快速调整
个性化推荐系统快速适应用户偏好 - 神经架构搜索(NAS)
学习如何设计有效网络架构 - 超参数优化
学习如何调整学习率等超参数
- 小样本学习(Few-shot Learning)
- 优势与挑战
- 优势
- 数据效率高,减少对大规模标注数据的依赖
- 适应速度快,适合动态变化的环境
- 泛化能力强,能处理未见过的任务类型
- 挑战
- 任务分布假设严格,需要任务间的相似性
- 训练过程计算量大,需要大量元训练任务
- 容易过拟合到元训练任务分布
2. 四种解决“数据稀缺”问题的小样本轴承故障诊断方法
(1)迁移学习 (Transfer Learning)
- 核心思想:利用旧知识(源领域) 帮助学习新任务(目标领域),前提是两者之间存在相似性。模型先在数据充足的相关任务上进行预训练,学到的通用特征或模型参数再被迁移到数据稀缺的新故障诊断任务上,从而提升学习效率和性能。
- 论文中的评价:这类方法的效果高度依赖于源任务和目标任务之间数据分布的相似性以及距离函数的选择。在实际工业场景中,不同工况下的故障数据分布差异可能很大,因此如何选择合适的源领域和距离度量是一个挑战。
(2)数据增强 (Data Enhancement / Augmentation)
- 核心思想:在不引入新样本的前提下,通过对有限的原始样本进行变换或生成,创造出新的、多样化的训练数据,从而让模型从“等价于更多的样本”中学习,缓解过拟合。
- 常用技术:
生成对抗网络 及其变体(如WGAN)
变分自编码器 - 论文中的评价:这是解决小样本问题最直接的方法。但它存在一些固有问题:
模型训练困难(如GAN训练不稳定)。
梯度消失/爆炸。
难以保证生成样本的质量和多样性,如果生成样本质量差,反而会引入噪声,损害模型性能。
(3)度量学习 (Metric Learning)
- 核心思想:训练模型学习一个具有判别性的特征空间(嵌入空间)。在这个空间中,同类故障样本的特征彼此接近,不同类故障样本的特征彼此远离。诊断时,通过计算新样本与各类别原型(如类中心)或支持集样本之间的相似度来进行分类。
- 论文中的评价:这类方法的关键在于如何设计或选择有效的相似性度量函数(如欧氏距离、余弦相似度)。方法的性能严重依赖于度量函数的好坏,而在不同的故障诊断任务中,设计一个普适且高效的度量函数是具有挑战性的。
(4)元学习 (Meta-Learning)
- 核心思想:其目标是“学会如何学习”。通过在大量相似的小样本任务上进行训练,让模型掌握快速适应新任务的能力。当遇到一个全新的、只有少数样本的故障诊断任务时,模型能够通过少量梯度更新或示例比对迅速达到高性能。
- 主流分支(基于优化的元学习):
学习一组良好的模型初始化参数(如MAML),使得从该初始点出发,对新任务进行几步微调就能取得好效果。
学习一个优化器。 - 论文中的评价:元学习旨在提升模型的泛化能力和快速适应性,特别适合小样本学习。但文中也指出,经典方法如MAML存在对复杂任务的学习能力不足和训练难度大的问题。
论文工作的定位:
本文提出了一种基于脑启发的元学习方法,旨在克服传统元学习方法在复杂轴承故障诊断任务中的局限性,通过引入脑电信号的辅助信息,提升模型在少样本条件下的诊断性能和适应能力。
现有研究的空白:
(1)脉冲神经网络 在生物学可解释性和能效方面有优势,但其脉冲序列的非连续性使其难以直接应用主流的反向传播算法。
(2)现有的SNN故障诊断方法,其学习策略本质上是反向传播算法的变体,而非对生物大脑学习机制的模拟,因此不具备生物大脑那样强大的小样本学习能力。
因此提出 BIML(基于脑启发的元学习策略),其创新点在于:
学习机制创新: 基于生物神经系统的脉冲时序依赖可塑性 和自上而下调节信号,设计了一种全新的、更具生物可解释性的权重更新方法,而非模拟BP算法。
框架创新: 将这种脑启发的权重更新方法与元学习策略相结合,使模型能够真正模拟大脑“从经验中学习如何快速学习”的能力,从而更好地解决小样本轴承故障诊断这一实际问题。
3. “N-way K-shot”学习任务
专门用于定义和评估小样本学习模型的性能。
- N-way: 表示在每个任务中,模型需要从 N 个不同的类别 中进行区分和分类。
在本文中,N = 9。这对应着轴承的 9 种健康状态(1种正常状态 + 3种故障类型 × 不同程度的故障 = 8种故障状态,具体由数据集定义)。 - K-shot: 表示在模型进行学习(训练或适应)时,每个类别仅提供 K 个带标签的样本作为参考。
K = 1 就是 1-shot,每个类别只有1个例子。
K = 5 就是 5-shot,每个类别有5个例子。
所以:
9-way 1-shot task:一个任务中,模型面对9种不同的轴承状态,但用于学习每种状态的参考样本只有1个。这是极端的小样本学习场景,对模型要求极高。
9-way 5-shot task:同样面对9种状态,但每种状态有5个参考样本。这比1-shot提供了更多信息,任务相对容易一些,但仍然是典型的小样本场景。
论文实验中的具体操作
- 数据准备:
每种工况下,每种健康状态采集了100个数据样本(使用1024点的滑动窗口)。
- 对于 9-way 1-shot 任务:
- 支持集:从每个类别的100个样本中,随机挑选1个。所以支持集总共有 9类 × 1个/类 = 9个样本。
- 查询集:剩下的 100 - 1 = 99个样本。查询集总共有 9类 × 99个/类 = 891个样本。
- 对于 9-way 5-shot 任务:
- 支持集:从每个类别的100个样本中,随机挑选5个。支持集总共有 9类 × 5个/类 = 45个样本。
- 查询集:剩下的 100 - 5 = 95个样本。查询集总共有 9类 × 95个/类 = 855个样本。
- 元学习训练与评估流程:
- 支持集 用于 内层更新:在元学习循环中,模型用这极少量的样本(9个或45个)来模拟“快速适应”一个新任务。
- 查询集 用于 外层更新 和 最终评估:
- 在元训练阶段,用查询集计算损失来更新初始参数(元学习的关键步骤)。
- 在最终测试阶段(例如,对一个全新的、未见过的工况),模型在目标任务的支持集上微调后,在其查询集上计算准确率,作为模型性能的最终指标。



